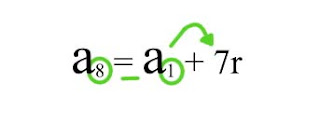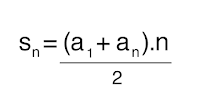Progressão aritmética: fórmula, exercícios e exemplos

Se você está começando os estudos do tema progressão aritmética, ou já estudou mas ainda não domina o assunto, então você deve assimilar inicialmente o conceito mais básico possível.

Saiba simplesmente que progressões aritméticas não passam de sequências numéricas. Por exemplo, lembre-se dos períodos em que ocorrem as Olimpíadas. Elas são realizadas a cada quatro anos. Assim, os Jogos Olímpicos ocorreram nos anos de 2008, 2012, 2016, 2020. 

Como não há uma data para o fim do mundo 😎 (nem das Olimpíadas), então nós podemos considerar essa sequência como infinita, ou seja, uma progressão aritmética infinita.

Agora imagine os meses do ano, que começam em 01 e terminam em 12. Temos aqui uma progressão aritmética finita.

Esses são dois exemplos práticos de progressão aritmética.

No nosso estudo, vamos conceituar detalhadamente o que é PA, assim como iremos estabelecer a sua fórmula e ilustrar o conteúdo com muitos exemplos e exercícios.

Após ler todo o conteúdo, situe-se no texto mais facilmente através do índice abaixo.

{getToc} $title={Índice da aula textual}

O que é um progressão aritmética PA

Antes mesmo de perguntar o que é uma progressão aritmética, a qual também é conhecida pela abreviação PA, você deve pensar e indagar sobre o que é progressão.

O que é uma progressão

De acordo com os dicionários, progressão é o desenvolvimento gradual de um processo; sucessão. Ou seja, PA é uma sucessão numérica que ocorre gradualmente, como os degraus de uma escada.

O que é aritmética

Por sua vez, temos que desvendar o que vem a ser a palavra aritmética. Trata-se da parte da matemática que lida com as operações numéricas: soma, subtração, divisão e multiplicação.

Depois da análise separada dos termos estudados, agora já somos capazes de conceituar o que é uma progressão aritmética: sequência numérica em que a diferença entre um termo e o termo anterior é constante. Logicamente a diferença é contabilizada a partir do segundo termo da PA.

A essa diferença damos o nome de razão, a qual é constante, isto é, o valor da razão é sempre o mesmo.

A seguir, vejamos um exemplo para clarear as ideias.

Progressão aritmética exemplos

Tudo pode parecer meio complicado à primeira vista, mas acredite: não é!

Observe e comprove isso através do exemplo citado no início desta aula textual: os anos em que ocorrem as Olimpíadas.

Nós já mencionamos que elas aconteceram, entre outros, nos anos: 2008, 2012, 2016, 2020.

Essa sequência de números é uma progressão aritmética crescente (observe que os números estão crescendo gradativamente).

Já sabemos que as Olimpíadas ocorreram em anos anteriores a 2008, bem como serão realizadas em anos posteriores a 2020.

Porém, vamos delimitar apenas esses quatro anos, a fim de facilitar a compreensão.

Prosseguindo, é importante dar nome aos bois, ou seja, devemos estabelecer quem é quem nesta PA.

Note inicialmente que temos quatro termos na progressão. Cada ano corresponde a um termo.

Diante disso, já podemos delimitar o número de termos: 4.

Outra coisa muito relevante é a posição dos anos (termos da PA): 2008, 2012, 2016, 2020.

O primeiro termo é 2008 e o quarto é 2020.

Preste bastante atenção porque os termos de uma PA não são estabelecidos aleatoriamente, mas em uma ordem rigorosamente respeitada. 

Nós devemos denominar o primeiro termo (2008) de a_1.

O segundo termo será o a₂ e assim por diante. Mas tudo isso será detalhadamente explicado no decorrer da aula textual.

Assim, saber claramente a posição de determinado termo integrante da progressão aritmética é crucial para se evitar erros de cálculos.

Agora perceba, por fim, que a diferença entre um termo da PA e o termo imediatamente anterior é sempre igual a 4.

Exemplos:

2012 - 2008 = 4.

2020 - 2016 = 4.

Aí vai uma ótima notícia: todos os conceitos estabelecidos nesta PA exemplificativa se aplicam a qualquer progressão aritmética.

Isso significa, inclusive, que podemos estabelecer uma fórmula aplicável a qualquer PA, independentemente do número de termos.

Fórmula da progressão aritmética

Vamos continuar a usar o nosso exemplo como parâmetro, a fim de extrairmos a fórmula da progressão aritmética, também conhecida como termo geral da PA.

Poderíamos simplesmente escrever aqui o termo geral da progressão aritmética, mas isso não faria o menor sentido, pois você iria apenas decorar a fórmula, sem entender como ela é construída e como é usada.

Com certeza, é sempre melhor aprender do que decorar! O risco de esquecer algo que foi apenas decorado é muito grande.

Inicialmente devemos conhecer as letras que substituirão os números, a fim de nos familiarizarmos com elas. 

Depois disso explicaremos como a fórmula é constituída.

Número total de termos da progressão aritmética

Já sabemos que a nossa PA referente aos anos em que ocorreram as Olimpíadas tem 4 termos, entretanto, se não soubéssemos o número total de termos de uma PA genérica, diríamos então que a progressão aritmética tem n termos.

Então você deverá sempre recordar que n será o número total de termos da progressão aritmética.

Posição de cada termo na progressão aritmética

Avançando, vamos chamar cada termo representado pelos anos de a.

Então:

2008 = a₁

2012 = a₂

2016 = a₃

2020 = a₄

Observe que depois da letra a temos os números variando de 1 a 4.

Isto também é de fundamental importância porque eles representam a posição ocupada pelo termo específico na PA. 

Por exemplo, a₃ corresponde ao terceiro termo da progressão. Lê-se também: a índice 3.

Agora vamos supor que não sabemos a posição de determinado termo em um PA genérica. Neste caso, chamaremos esse número de a. Assim, teremos o termo genérico a_n, que pode  ser lido como a índice n ou enésimo termo.

Veremos a seguir que as posições dos termos na PA são essenciais para fazermos os cálculos por meio da fórmula da progressão aritmética.

Para assimilar bem a importância da posição sequencial dos termos, imaginemos a seguinte situação hipotética do salto de um paraquedista. Existe um passo a passo: 1 - o paraquedista embarca no avião; 2 - o avião decola; 3 - o paraquedista salta do avião; 4 - no momento ideal, o paraquedista abre o paraquedas.

O salto somente será bem sucedido se a ordem descrita for respeitada, principalmente em relação aos itens 3 e 4. Já pensou se o paraquedista abre o paraquedas ainda  dentro do avião e salta depois? Como diria o Sr. Omar do Todo mundo odeia o Cris: trágico!

Razão da progressão aritmética

No nosso exemplo, se realizarmos uma subtração entre determinado termo da progressão (a partir do segundo termo) e o termo imediatamente anterior, teremos sempre o valor 4.

Olhe: 

2012 - 2008 = 4;

2016 - 2012 = 4.

2020 - 2016 = 4.

Pois bem, o resultado dessa subtração será sempre o mesmo na PA, ou seja, esse valor é chamado de razão da PA e será sempre constante.

Olhando novamente a PA:

2008, 2012, 2016, 2020

Se quisermos descobrir qual será próximo termo dessa progressão, basta irmos somando sucessivamente o valor do termo com o valor da razão (4). Assim:

2008, 2012, 2016, 2020, 2024, 2028 ...

Da mesma forma, se quiséssemos descobrir os valores anteriores a 2008, seria necessário ir subtraindo os termos sucessivamente pelo valor da razão (4). Repare:

... 1996, 2000, 2004, 2008, 2012, 2016

No nosso exemplo, o valor da razão da PA é sempre 4. Mas, supondo que estamos lidando com valores genéricos, chamaremos a razão de r.

Progressões crescente, constante e decrescente

De acordo com o valor da razão, as PAs podem ser classificadas como crescente, constante e decrescente.

• Quando a razão for maior que zero, r > 0, a PA será crescente.
• Quando a razão for igual a zero, r = 0, a PA será constante.
• Quando a razão for menor que 0, r < 0, a PA será decrescente.

Vejamos alguns exemplos.

👉 2, 4, 6, 8, 10, 12 ...

Temos aqui uma progressão aritmética crescente, pois a sua razão é 2, que é maior que zero.

Sabemos disso através da subtração de um termo (a partir do segundo) pelo termo anterior.

Comprovando: 4 - 2 = 2; 6 - 4 = 2, 8 - 6 = 2 etc.

Agora preste atenção na seguinte PA:

👉 3, 3, 3, 3, 3 ...

Estamos aqui diante de uma progressão aritmética constante, cuja razão é zero.

Comprovando: 3 - 3 = 0; 3 - 3 = 0 etc.

Finalizando, confira a progressão seguinte:

👉 20, 15, 10, 5, 0, -5, -10, -15, -20 ...

Nota-se neste momento uma progressão aritmética decrescente, tendo em vista que sua razão é -5, ou seja, menor que zero.

Chegamos a este resultado subtraindo determinado termo pelo seu termo anterior.

Comprovando: 15 - 20 = -5; 0 - 5 = -5; -10 - (-5) = -10 + 5 = -5 etc.

Construindo a fórmula da PA

Agora já conhecemos todas as possíveis variáveis da fórmula de uma progressão aritmética (P.A).

Resta apenas sabermos como essa formula é montada e como ela pode ser aplicada posteriormente a qualquer PA.

🖐 Se o texto estiver extenso, pare um pouco, beba uma água, respire e continue. Aprender é assim mesmo, requer esforço mental. 

Mas pode ter certeza que, para se chegar aonde os outros não chegam é preciso fazer o que os outros não fazem. Todo esforço será recompensado se você persistir.

Recomponha-se e mãos à obra!

Relembrando o que já vimos nesta textoaula:

➡ Chamamos o número total de termos da PA de n.

➡ Chamamos cada termo em sua posição específica de a_n (lê-se a índice n ou enésimo termo da PA).

➡ Chamamos a razão de r.

Agora você já sabe como nós descobrimos o valor da razão de uma PA (subtraindo um termo pelo seu antecessor).

Por isso, você já é capaz de entender tudo se usarmos letras em vez de números.

Pois bem, imaginemos agora a seguinte progressão aritmética crescente:

👉 2, 5, 8, 11, ...

Perceba que já temos 4 termos expressos:

a₁, a₂, a₃, a_4, ...

A razão desta PA é calculada da mesma forma, subtraindo um termo pelo termo antecedente.

Então:

r = a₂ - a₁

ou 

r = a₃ - a₂ e assim por diante.

Vamos calcular...

r = a₂ - a₁

r = 5 - 2

r = 3

Depois de descobrir o valor da razão, podemos descobrir o valor de qualquer termo da PA. Isso é fantástico!

Por exemplo, se tu queres saber qual é o oitavo termo, isto é, o a₈, basta efetivar a adição dos termos com a razão até chegar ao 8º termo.

Já sabemos qual é o quarto termo (a₄) e poderemos calcular, adicionando os valores da razão, a partir dele.

Vamos lá!

a₅ = a₄ + r = 11 + 3 = 14

a₆ = a₅ + r = 14 + 3 = 17

a₇ = a₆ + r = 17 + 3 = 20

a₈ = a₇ + r = 20 + 3 = 23

Pronto! Chegamos ao valor do oitavo termo da nossa PA, isto é, a₈ = 23.

Note que deu um trabalhinho, não é mesmo?!

Tivemos que ir somando cada um dos termos com a razão.

Repare ainda que fizemos isso quatro vezes.

Imagine se quiséssemos descobrir o centésimo termo desta PA? Já pensou na trabalheira?

Mas a boa notícia é que não precisamos somar o valor da razão várias vezes!

No exemplo acima, ao invés de somar a razão quatro vezes, conforme já fizemos:

a₄ + r

a₅ + r

a₆ + r

a₇ + r

Vamos simplificar fazendo simplesmente o seguinte:

a₈ = a₄ + 4r

Agora só falta substituir os valores que já conhecemos.

a₈ = a₄ + 4r

a₈ = 11 + 4 x 3 

a₈ = 11 + 12

a₈ = 23

Chegamos ao mesmo resultado usando um cálculo bem mais rápido, simples e fácil.

Agora vem o pulo do gato!

Imagine que, ao invés de sabermos os valores dos termos vistos na PA que estamos examinando, soubéssemos apenas quais são os dois primeiros termos?

Ou seja, a₁ e a₂?

Veja:

👉 2, 5, ...

Obviamente o trabalho para se descobrir o oitavo termo (A8) seria ainda maior:

a₁ = 2

a₂ = a₁ + r = 2 + 3 = 5

a₃ = a₂ + r = 5 + 3 = 8

a₄ = a₃ + r = 8 + 3 = 11

a₅ = a₄ + r = 11 + 3 = 14

a₆ = a₅ + r = 14 + 3 = 17

a₇ = a₆ + r = 17 + 3 = 20

a₈ = a₇ + r = 21 + 3 = 23

O trabalho aumentou substancialmente porque tivemos agora que somar a razão sete vezes a diversos termos da progressão.

Mas isso pode novamente ser evitado se, ao invés de somarmos sete vezes a razão (r + r + r + r + r + r + r), aplicarmos apenas a multiplicação 7 x r. 

Depois basta somarmos tudo ao primeiro termos da PA:

a₈ = a₁ + 7r

a₈ = 2 + 7×3

a₈ = 2 + 21

a₈ = 23

De novo, nós atingimos o valor idêntico para o oitavo termo, o que comprova a efetividade e a confiabilidade do cálculo.

Finalmente estamos prontos para concluir a fórmula da progressão aritmética, que como já mencionamos também é conhecida como termo geral da PA.

Preste bastante atenção ao último cálculo realizado:

a₈ = a₁ + 7r

Já esclarecemos no decorrer da exposição que em uma PA genérica atribuiríamos a letra n a um termo inserido em uma posição genérica. Chegou a hora de colocarmos isto em prática.

No caso acima estávamos buscando o oitavo termo (específico), por isso usamos o a₈. Contudo, se estivéssemos em busca do enésimo termo (genérico), então deveríamos a_n.

Observe mais uma vez:

a₈ = a₁ + 7r

Veja que o número que acompanha a variável r é 7 e o número que acompanha a primeira variável a é 8.

Isso nos leva a uma conclusão lógica: o valor que acompanha o r é uma unidade a menos que o número que acompanha o primeiro a.

Outra forma de raciocínio possível é subtrair 8 - 1 para sabermos qual o valor que acompanha o r na fórmula. Veja:

Transformando essas constatações para uma linguagem matemática, é o mesmo que dizer:

a_n = a₁+ (n - 1) * r

Eureca! Agora você já sabe de onde saiu a fórmula da progressão aritmética, ou seja, o termo geral, onde:

• a_n 👉 enésimo termo
• a₁ 👉 primeiro termo
• n 👉 número total de termos
• r 👉 razão

Foi um longo caminho até aqui, mas a recompensa é enorme, pois você será capaz de descobrir o valor de qualquer termo de uma PA.

Como exemplo, vamos retomar a nossa PA em analise:

👉 2, 5, ...

Vamos calcular o valor do quinto termo através da fórmula...

a_n = a₁+ (n - 1) * r

Apenas olhando para a PA, é possível sabermos que:

a₁ = 2

r = 3

Queremos descobrir o quinto termo, então basta substituir n por 5 e os demais valores na fórmula.

a₅ = 2 + (5 - 1) * 3

a₅ = 2 + 4 * 3

a₅ = 2 + 12

a₅ = 14.

Retorne no texto ao ponto em que fizemos tudo de forma manualmente primitiva e irá constatar que o valor está correto.

E se quisermos descobrir o centésimo termo da nossa progressão?

Agora ficou fácil com a fórmula!

Basta substituir os valores;

a₁₀₀ = 2 + (100 - 1) * 3

a₁₀₀ = 2 + 99 * 3

a₁₀₀ = 2 + 297

a₁₀₀ = 299

Tudo ficou claro e objetivo. Se você quiser saber o valor de qualquer termo, o milionésimo por exemplo, é possível por meio da fórmula PA.

Inclusive dá até para brincar com PAs construídas com letras e números. Por sinal, as provas de matemática gostam muito dessa brincadeira.

Veja uma PA hipotética:

👉 x + 1, x + 2, ...

Vamos descobrir por exemplo o valor do quinto termo.

Quando estamos diante de PAs desta natureza, a primeira coisa a se fazer é descobrir o valor da razão r. 

Já sabemos que razão é a diferença entre um termo e o seu antecessor.

a₁ = x +1

a₂ = x+2

Esquematizando:

r = a₂ - a₁

r = (x + 2) - (x + 1)

r = x + 2 - x - 1

r = x - x + 2 - 1

r = 1

Agora que já sabemos o valor da razão, basta substituí-lo na fórmula juntamente dos valores que já conhecemos.

a_n = a₁+ (n - 1) * r

a₅ = x + 1 + (5 - 1)*1

a₅ = x + 1 + 4*1

a₅ = x + 1 + 4

a₅ = x + 5

Portanto, o quinto termo da nossa progressão aritmética é x + 5.

Extensão do termo geral da progressão aritmética

Vimos inicialmente que a fórmula do termo geral da PA envolve obrigatoriamente o primeiro termo a₁.

No entanto, podemos estender a fórmula do termo geral para quaisquer termos, basta substituir 1, referente ao primeiro termo, pela variável k (pode ser qualquer letra). Olhe:

a_n = a_k+ (n - k) * r

Isso quer dizer que podemos fazer os cálculos que desejarmos a partir de qualquer termo que não seja o primeiro.

Já vimos uma aplicação prática bem lá em cima no texto. Mas vamos retomá-la para simplificar. Veja então a PA que exploramos:

👉 2, 5, 8, 11, ...

Já calculamos o oitavo termo, a partir do quarto, da seguinte forma:

a₈ = a₄ + 4r

a₈ = 11 + 4 * 3

a₈ = 11 + 12

a₈ = 23

Veja como o cálculo é perfeitamente compatível com o termo geral estendido:

Na fórmula do termo geral, usa-se a₁, porém no termo geral estendido pode-se usar qualquer termo conhecido da PA, ou seja: a_{k .}

Em uma linguagem bem técnica, dizemos que é possível se calcular o enésimo termo a partir do k-ésimo termo de uma progressão aritmética.

Agora, a título de exemplo, vamos calcular o décimo termo da PA através da fórmula estendida, tomando como base o quarto termo (a₄).

a_n = a_k + (n - k)*r

a₁₀ = a₄ + (10 - 4)*3

a₁₀ = 11 + 6*3

a₁₀ = 11 + 18

a₁₀ = 29.

Vamos conferir?

👉 2, 5, 8, 11, 14, 17, 20, 23, 26, 29, ...

Para entender mais facilmente a fórmula estendida ou generalizada, imaginemos que queiramos descobrir o nono termo a partir do segundo termo. Fica assim:

a₉ = a₂ + (9 - 2)*r

Note que basta subtrair o 9 que acompanha o primeiro a pelo 2 que acompanha o segundo a.

Da mesma forma, se o primeiro a estiver acompanhado de n e o segundo a estiver acompanhado de k, basta inserirmos estas variáveis na fórmula.

a_n = a_k+ (n - k) * r

Soma dos termos da progressão aritmética

É possível obtermos a soma de todos os termos de uma PA finita. 

A primeira pessoa que realizou essa façanha foi uma criança chamada Johann Carl Friedrich Gauss, que depois se tornou matemático, físico e astrônomo, um dos mais brilhantes, diga-se de passagem.

Soma de Gauss

Ainda quando criança, aproximadamente com dez anos de idade, Gauss e sua turma da escola foram punidos por determinado professor, tendo os alunos sido obrigados a somar todos os números inseridos na sequência de 1 a 100. 

Para a surpresa do professor e da turma, antes de todo mundo, Gauss resolveu o problema em alguns minutos, chegando ao resultado final de 5050.

Gauss obteve a rápida solução do problema depois de perceber que a soma dos extremos 1 e 100 é igual a 101.

Ele também percebeu que a soma do segundo número (2) com o penúltimo (99) também resulta em 101.

Por fim, ele constatou que a soma do terceiro número (3) com o antepenúltimo (98) também resultava em 101. 

Diante disso, Gauss supôs que todas as somas da sequência analisada resultariam em 101. Esquematizando o raciocínio do ilustre matemático:

Como o primeiro e o último número compõem um par de números e assim por diante, ele racionou que os 100 números formam 50 pares de números, ou seja, os números de pares correspondem à metade do número de elementos da sequência.

Então ele fez um cálculo simples: multiplicou a quantidade de pares de números (50) pela valor que correspondia às somas de cada um desses pares (101).

Assim:

50 x 101 = 5050

Por causa desse raciocínio, surgiu a fórmula que possibilita a soma dos termos de uma PA:

A fórmula supracitada também é conhecida como somatório geral da progressão aritmética.

Propriedades da Progressão Aritmética

Propriedade #01

Em uma P.A. finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.

Vejamos um exemplo para facilitar o entendimento:

Os extremos desta P.A. são os números 2 e 20. A palavra equidistante significa algo que está posicionado exatamente na mesma distância.

Assim os equidistantes dos extremos são o segundo e o penúltimo termos, no caso, os números em azul 5 e 17.

Também temos o terceiro e o antepenúltimo termos como equidistantes (em vermelho), no caso 8 e 14.

Pois bem as somas dos extremos resulta em 22 (2 + 20).

Da mesma forma, a soma dos equidistantes: 5 + 17 = 22; 8 + 14 = 22.

Essa propriedade também decorre do célebre raciocínio realizado pelo matemático Gauss.

Propriedade #02

Considerando a existência de três termos consecutivos de uma P.A., o termo do meio será exatamente igual a média aritmética dos outros dois termos.

Veja no exemplo:

Propriedade #03

Em uma P.A. finita e construída com número de termos ímpar, o termo central da progressão será igual a média aritmética entre termos equidistantes deste. Esta propriedade é decorrente da primeira.

Vejamos um exemplo:

Progressão aritmética exercícios

Vejamos agora como o conteúdo de progressões aritméticas é cobrado em provas de concursos públicos, bem como do Exame Nacionao do Ensino Médio - Enem.

Exercício #01

(Prefeitura de Alto Bela Vista/SC - AMAUC - 2021 - Técnico em Enfermagem) Sobre a Progressão Aritmética (PA) a seguir, assinale a alternativa incorreta:

23, 32, 41, 50, 59, 68, ...

a) A razão da PA é igual a 9.

b) Para aplicar a fórmula do somatório dos termos da PA, se faz necessário o conhecimento de sua razão.

c) O trigésimo termo da PA é igual a 284.

d) O trigésimo quinto termo da PA é igual a 263.

e) O somatório dos dez primeiros termos da PA é igual a 635.

Letra a: correta. Para descobrirmos o valor da razão é muito simples. Basta extrairmos a diferença a partir da subtração de um termo da PA pelo termo antecedente. Por exemplo: 32 - 23 = 9.

Letra b: correta. A fórmula da soma dos termos de uma PA não requer necessariamente o valor da razão r. Precisamos saber apenas os valores correspondentes às variáveis n, a₁ e a_n. Relembre: s_n = (a₁ + a_n)n/2.

Porém, em relação especificamente ao caso tratado na questão, não sabemos qual é o valor de a_n e somente podemos descobri-lo através da fórmula do termo geral. Esta sim requer o valor da razão para realização dos cálculos. Veja: a_n = a₁+ (n - 1) * r. Por isso a alternativa está correta.

Letra c: correta. Para calcularmos o trigésimo termo, basta utilizarmos a fórmula do termo geral da progressão aritmética:

a_n = a₁+ (n - 1) * r

a₃₀ = 23 + (30 - 1) * 9

a₃₀ = 23 + 29 * 9

a₃₀ = 23 + 261

a₃₀ = 284

Letra d: incorreta. Como a progressão dada na questão é crescente e o trigésimo termo é 284, não há como o trigésimo quinto ser menor, ou seja, 263. Aplicando-se o termo geral da PA, iremos constatar que o trigésimo quinto termo da progressão aritmética é 329.

Letra e: correta. Antes de calcularmos a soma dos dez primeiros termos desta P.A., temos que descobrir o valor do décimo termo (a₁₀).

Mais uma vez, é suficiente o emprego da fórmula da progressão aritmética:

a_n = a₁+ (n - 1) * r

a₁₀ = 23 + (10 - 1) * 9

a₁₀ = 23 + (9) * 9

a₁₀ = 23 + 81

a₁₀ = 104

Agora vamos calcular a soma dos dez primeiros termos.

s_n = (a₁ + a_n)*n/2

s_n = (23 + 104)*10/2

s_n = (127)*10/2

s_n = 635

A presente questão solicitou a identificação da alternativa incorreta. Neste sentido, apenas a letra d está errada.

Portanto, gabarito: letra d.

Passemos ao próximo exercício.

Exercício #02

(CESPE - 2021 - SEDUC-AL - Professor - Matemática) Cada um do próximo item apresenta uma situação hipotética a ser julgada, acerca de problemas matemáticos envolvendo situações em uma escola.

Ao escrever uma redação, um aluno levou meia hora para escrever 885 palavras, tendo sido capaz de escrever 15 palavras no primeiro minuto desse tempo. Considerando-se que, a cada minuto, na quantidade de palavras que ele escrevia, era acrescida uma quantidade constante fixa de palavras ao número de palavras do instante anterior, então é correto concluir que, no último minuto, ele escreveu exatamente 44 palavras. 

Comentários!

A questão nos informa inicialmente que o aluno levou meia hora, ou seja, 30 minutos, para escrever 885 palavras.

Além disso, o aluno escreveu 15 palavras no primeiro minuto e a cada minuto que passava ele escrevia uma quantidade constante a mais de palavras.

Para resolvermos a questão, basta que usemos a fórmula do somatório dos termos da PA: 

s_n = (a₁ + a_n)*n/2

O enunciado já nos forneceu todas as informações capazes de resolver o problema, inclusive que a soma total de palavras escritas durante 30 minutos é 885.

Vamos organizar os dados:

n = 30 minutos

a₁ = 15 minutos

s_n = 885 palavras

No final, o enunciado da questão afirma que no último minuto, ou seja, no trigésimo, o aluno escreveu exatamente 44 palavras.

Então, para julgarmos se isso está certo ou errado, temos que conferir se o trigésimo termo, ou seja, o a₃₀, corresponde ou não a 44.

então...

s₃₀ = (a₁ + a₃₀)*30/2

885 = (15 + a₃₀)*15

885/15 = (15 + a₃₀)

59 = (15 + a₃₀)

59 - 15 = a₃₀

a₃₀ = 44

Portanto, no trigésimo minuto, o aluno realmente escreveu 44 palavras. 

Gabarito: correto.

Exercício #03

(Instituto UniFil - 2021 - Prefeitura de Cambé - PR - Professor - Educação Infantil) Uma senha bancária com 6 dígitos foi formada com os termos a₅₀ e a₅₁ da progressão aritmética que tem razão r = 4 e o termo inicial a₁ = 3. Assinale a alternativa que apresenta a senha formada. 

a) 151154

b) 154157

c) 195199

d) 199203

e) 203207 

Comentários!

Esta questão é muito tranquila. A senha formada contém 6 dígitos e é constituída por dois termos de uma progressão aritmética: a₅₀ e a₅₁. 

Isso significa que cada termo terá obrigatoriamente 3 dígitos.

O enunciado nos informa o valor do primeiro termo (a₁ = 3) e da razão (r = 4) da progressão.

Vamos aos cálculos através da fórmula da PA.

a_n = a₁ + (n - 1) * r

a₅₀ = 3 + (50 - 1) * 4

a₅₀ = 3 + (49) * 4

a₅₀ = 3 + (49) * 4

a₅₀ = 3 + 196

a₅₀ = 199

Assim o quinquagésimo termo (a₅₀) é 199. Para acharmos o valor do quinquagésimo primeiro termo, basta somarmos mais uma vez do valor da razão. 

Assim,

a₅₁ = a₅₀ + r

a₅₁ = 199 + 4 = 203

Portanto, a senha formada é 199203.

Gabarito: letra d.

Exercício #04

(Objetiva - 2021 - Prefeitura de Pato Bragado - PR - Assistente Social) Considerando-se que certa progressão aritmética possui razão igual a 4 e que seu primeiro termo é igual a 24, assinalar a alternativa que apresenta o resultado da soma dos 8 primeiros termos dessa progressão:

a) 108

b) 152

c) 304

d) 608

Comentários!

Iniciaremos organizando os dados:

r = 4

a₁ = 24

s₈ = ?

Antes de tudo, temos que descobrir o valor de a₈ através do termo geral da progressão aritmética:

a_n = a₁+ (n - 1) * r

a₈ = 24 + (8 - 1) * 4

a₈ = 24 + (7) * 4

a₈ = 24 + 28

a₈ = 52

Agora vamos realizar o somatório dos oito primeiros termos através da fórmula correspondente.

s_n = (a₁ + a_n)*n/2

s₈ = (24 + 52)*8/2

s₈ = (76)*8/2

s₈ = 76*4

s₈ = 304

Portanto, a soma dos oito primeiros termos da progressão aritmética descrita no exercício é 304.

Gabarito: letra c.

Exercício #05

(Enem - 2019 - PPL) Em um município foi realizado um levantamento relativo ao número de médicos, obtendo-se os dados:

Tendo em vista a crescente demanda por atendimento médico na rede de saúde pública, pretende-se promover a expansão, a longo prazo, do número de médicos desse município, seguindo o comportamento de crescimento linear no período observado no quadro.

Qual a previsão do número de médicos nesse município para o ano 2040?

a) 387

b) 424

c) 437

d) 574

e) 711

Comentários!

Observe que a quantidade de médicos varia de vinte e cinco em vinte e cinco a cada cinco anos. Por exemplo, no ano 1980, a demanda era de 137 médicos. Já no ano de 1985 a demanda subiu para 162, ou seja, em 5 anos a acrescentou-se o total de 25 médicos.

De 1985 para 1995 (10 anos), a demanda de médicos aumentou para 50, ou seja, o que corresponde novamente a 25 médicos a cada 5 anos.

Isso significa que o número de médicos cresce em forma de progressão aritmética com os termos variando de vinte cinco em vinte e cinco. Em outras palavras, temos os termos variam com base na razão 25. 

A questão pergunta qual será a demanda de médicos no ano 2040.

Os anos são os termos da progressão, que varia de 5 em 5 anos.

Para descobrirmos o valor da quantidade de médicos no ano de 2040, devemos construir a PA referente aos anos correspondentes, variando de 5 em 5. Vamos organizar os dados:

1980, 1985, 1990, 1995, 2000, 2005, 2010, 2015, 2020, 2025, 2030, 2035, 2040.

Formou-se, portanto, uma progressão aritmética finita de 13 termos. Já temos o primeiro termo a₁, que corresponde a 137. 

Basta agora desvendarmos o valor do décimo terceiro termo a₁₃. Mais uma vez, iremos recorrer à fórmula da progressão aritmética:

a_n = a₁+ (n - 1) * r

a₁₃ = 137 + (13 - 1) * 25

a₁₃ = 137 + 12 * 25

a₁₃ = 137 + 300

a₁₃ = 437

Portanto, gabarito: letra c.

Acreditamos que foi abordado nesta oportunidade o que há de mais importante acerca do tema progressões aritméticas.

Veja tudo sobre um assunto bastante semelhante ao de PA:

• Progressões geométricas: fórmula, exercícios e exemplos

Bons estudos!